A mortality assumption is used in the actuarial present value calculation in order to determine the probability of death and survival in the future. While it is possible to use the mortality rates that have been provided in a published table, it is common for mortality rates to modified in various ways. EAC Tools allows a variety of ways to define the mortality parameter that is to be used in the functions.
Because 𝑙𝑥 is defined by a mortality table based on whole ages, it is necessary to obtain a value for 𝑙𝑥+𝑡 at a fractional age. A simple way of doing this is by assuming a uniform distribution of deaths (UDD) throughout the year of age 𝑥. This method is commonly used and is considered to be sufficiently accurate for all practical purposes.
To get detailed information about a specific type of mortality assumption, click its name in the first column.
|
Mortality Assumption |
The following are definitions of the basic actuarial mortality functions necessary to determine life expectancy and present value. Commutation functions are defined in another section of this document. The Social Security Administration has good description of life table functions.
The symbol (𝑥) denotes a life aged (𝑥).
Improvements in mortality can be applied by using a “set back age
adjustment” to a table. For example, with a 2-year setback, a 65 year old
person will have the mortality of a 63 year old.
where 𝑛 is the number of “set
back” years
Note: if 𝑛
<
0 then it is treated as a “set forward”.
More information on how to adjust a
mortality table with age set back adjustment (or a set forward)
is found here.
A mortality table can be adjusted by applying a factor to the table.
More information on how to
apply a factor to a mortality table is found here.
A new table can be created by blending two tables using weighting
factors for each table. For example, this is an easy way to create a unisex
table from underlying male & female tables.
More information on how to
blend two tables is
found here.
A new table can be created by combining two tables, where the first
table applies up to a given age, and the second table applies thereafter.
|
|
where 𝑎
is a given age at which the second table applies |
More information on how to combine two tables is found here.
Pre-retirement/post-retirement table
A pre-retirement/post-retirement table can be defined where one
table applies during the deferral period, and another table applies during the
payment period.
|
|
where c𝑎
is the given commencement age |
More information on how to define a pre-/post-retirement table is found here.
With a static mortality projection,
a mortality table is projected a number of years from the table’s base year to
a future year using a
mortality improvement scale that varies by age. The projected mortality rate is
determined by the following formula:
where 
annual
rate of mortality improvement from the one-dimensional improvement scale for age 𝑥.
More information on how to
project a table with a static mortality improvement scale is found here.
Generational mortality improvement
With a generational mortality projection, a mortality table is projected a number of years from the table’s base year to future years using a mortality improvement scale that:
· varies by age. The projected 1-dimensional mortality rate is determined by the following formula:
Where 𝑦 = the valuation year and annual
rate of mortality improvement from the one-dimensional improvement scale for
age 𝑥.
or,
· varies by age and year. The projected 2-dimensional mortality rate is determined by the following formula:
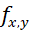
Where 𝑦 = the valuation year and 
is the annual rate of mortality improvement
from the two-dimensional improvement scale for age 𝑥 in year 𝑦.
More information on how to project a table with a 1-dimensional generational mortality improvement scale is found here.